Games
- There are many different kinds of games
- Deterministic or stochastic
- One, two, or more players?
- Zero sum?
- Perfect information (can you see the state)?
- We want algorithms for calculating a strategy (policy) which recommends a move from each state
Deterministic Games
- States
- Players
- Action
- Transition function
- Terminal test
- Terminal Utilities
Zero-sum games
- Zero-sum games
- Agents는 서로 반대되는 utilities(values on outcomes) 를 갖는다
- Let us think of a single value that one maximizes and the other minimizes
- Whatever is good for one is gonna be equally bad for the other. In such games, a utility is negative of the other’s
- Adversarial, pure competition
- General games
- Agents have 독립적인(independent) utilities (values on outcomes)
- Cooperation, indifference, competition, and more are all possible
- More later on non-zero-sum games
Adversarial Search
- Single-agent Trees
- Adversarial Game Trees
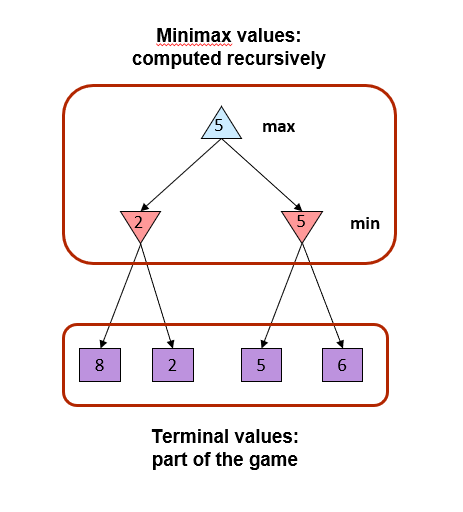
- Minimax
- A state-space search tree
- Players alternate turns
- Compute each node’s minimax value
- the best achievable utility against a rational (optimal) adversary
Alpha-Beta Pruning (가지치기)
- General Configuration (MIN version)
- 어떤 노드 n에서 Min-Value 계산
- We’re looping over n’s children
- n’s estimation of the childrens’ min is dropping
- Who cares about n’s value? MAX
- 뿌리에서 현재 경로를 따라 임의의 선택 지점에서 MAX가 얻을 수 있는 최상의 값을 a라고 할때, n이 a보다 나빠지면 MAX는 이를 피하므로 n의 다른 자식들을 고려하지 않을 수 있다. (it’s already bad enough that it won’t be played)
- Properties
- This pruning has no effect on minimax value computed for the root!
- 중간 노드의 값이 잘못되었을 수 있다
- 루트의 자식 노드는 잘못된 값을 가질 수 있다.
- 따라서 가장 naive version에서는 동작 선택을 할 수 없다.
- Good child ordering improves effectiveness of pruning
- With ‘perfect’ ordering
- 시간 복잡성이 O(b^(m/2))로 감소
- 해결 가능한 깊이가 두 배 증가
Resource Limits
- Problem
- In realistic games, cannot search to leaves
- Solution
- Depth-limited search
- 대신 트리에서 제한된 깊이만큼만 검색
- Terminal utilities를 터미널이 아닌 위치에 대한 평가 기능으로 대체
- Guareantee of optimal play is gone
- More plies makes a BIG difference
- Use iterative deepening for an anytime algorithm
Evaluation Functions
- Evaluation functions
- score non-terminals in depth-limited search
- Ideal function
- returns the actual minimax value of the position
- In practice
- typically weighted linear sum of features
Depth Matters
- 평가 함수는 항상 불완전함
- 평가 함수가 트리 깊숙한 곳에 있을 수록 평가함수의 품질은 중요하지 않음
- Features와 computation의 복잡성 사이의 절충을 보여주는 좋은 예시
Synergies between Evaluation Function and Alpha-Beta?
- Alpha-Beta: 확장 순서에 따라 pruning의 양이 달라짐
- 평가 함수는 가장 promising한 노드로 확장 (나중에 루트로 가는 경로에 이미 좋은 대안이 있을 가능성이 높아짐)
- Alpha-Beta (Similar for roles of min-max swapped)
- min-node의 값은 계속 감소
- 뿌리 노드로의 경로를 따라 최소 노드의 값이 더 나은 최대 옵션보다 낮으면, pruning 가능
- 따라서 평가 함수가 최소 노드의 값에 대한 상한선을 제공하고, 뿌리 노드로의 경로를 따라 최대 값에 대한 더 나은 옵션보다 상한선이 낮으면, pruning 가능
Summary
- Adversarial search
- Two agents playing zero-sum game, one maximizing the value while the other minimizing
- Adversarial search tree with minimax values allows to find the best achievable utility against an optimal opponent
- Alpha-beta pruning improves efficiency
- Evaluation functions approximate the utility from non-terminal nodes to mitigate resource limits issues.
'인공지능 > Artificial Intelligence (COSE361)' 카테고리의 다른 글
| [인공지능] Chapter 9. Markov Decision Process (1) (1) | 2023.10.25 |
|---|---|
| [인공지능] Chapter 8. Adversarial Search (2) (0) | 2023.10.25 |
| [인공지능] Chapter 6. Constraint Satisfaction problems (2) | 2023.10.24 |
| [인공지능] Chapter 5. Propositional logic (0) | 2023.10.24 |
| [인공지능] Chapter 4. Local Search (7) | 2023.10.24 |
