Basic Laws
- Uncertainty
- 예측 불가능한 실제 상황 ex. 비행기 출발 시간 1시간 전에 공항에 도착해야하는 상황
- 문제점
- Partial Observability (부분 관측성)
- 모든 정보를 전부 알 수 없는 상태
- ex. 도로 상태, 다른 운전자들의 계획
- Noisy Sensors (잡음이 많은 센서)
- 라디오 교통 정보나 구글 맵 같은 정보들이 항상 정확하지 않을 수 있음
- Complexity of Modelling and Predictiong (모델링과 예측의 복잡성)
- 교통, 대기 상태 등을 모델링 하고 예측 하는 것은 매우 복잡
- Lack of Knowledge of World Dynamics
- 예측하지 못한 사건의 발생
- Probabilistic Assertions (확률적 주장)
- ignorance(무지)와 laziness(게으름)의 영향
- ignorance (무지): 충분한 정보가 없음
- laziness (게으름): 정보를 얻기 위한 노력을 하지 않음
- Decision Theory (결정 이론)
- Probability theory (확률 이론) + Utility theory (효용 이론) → 최적의 결정
- 각각의 가능한 결정에 대한 예상 효용을 최대화하는 것을 목표로 함
- Maximize expected utility (예상 효용 최대화)
- Partial Observability (부분 관측성)
- Basic Laws of Probability (Discrete)
- Ω (a set of possible worlds, 가능한 세계의 집합)
- ex. 주사위를 던졌을 때 가능한 6가지 경우
- 𝑃(𝜔) (확률 모델)
- 각 가능한 세계 𝜔에 대한 확률
- 특정 결과 𝜔가 발생할 상대적인 가능성
- 0≤𝑃(𝜔)≤1 → 확률은 0~1 사이
- ∑_(𝜔∈Ω)〖𝑃(𝜔)〗=1 → 모든 확률 경우의 합은 1
- Event (사건)
- Ω(표본 공간)의 부분 집합
- 사건의 확률
- 그 사건을 구성하는 결과들의 확률의 합
- De Finetti의 법칙
- 확률을 잘못 적용하여 베팅하는 사람은 장기적으로 모든 베팅 세트에서 돈을 잃게 될 것
- Ω (a set of possible worlds, 가능한 세계의 집합)
- Random Variables (확률 변수)
- Some aspect of the world about which we may be uncertain
- ex. 주사위의 결과, 기온 등
- Deterministic Function (확정적 함수)
- 가능한 세계 상태(w)에 대한 확정적 함수
- 특정 상태에 대해 항상 동일한 결과값을 반환
- 값의 범위 (range)
- 확률 변수의 범위는 그 변수가 취할 수 있는 가능한 모든 값의 집합
- ex. Odd → 주사위가 홀수인지, 값은 참 또는 거짓
- T → 날씨가 덥거나 추운지, 값은 hot, cold가 될 수 있음
- D → 공항까지 가는 데 걸리는 시간, 값은 [0, 무한대)가 될 수 있음
- 확률 분포 (Probability Distribution)
- 확률 변수 X의 확률 분포 → 그 변수가 범위 내에서 각각의 값 x를 취할 확률
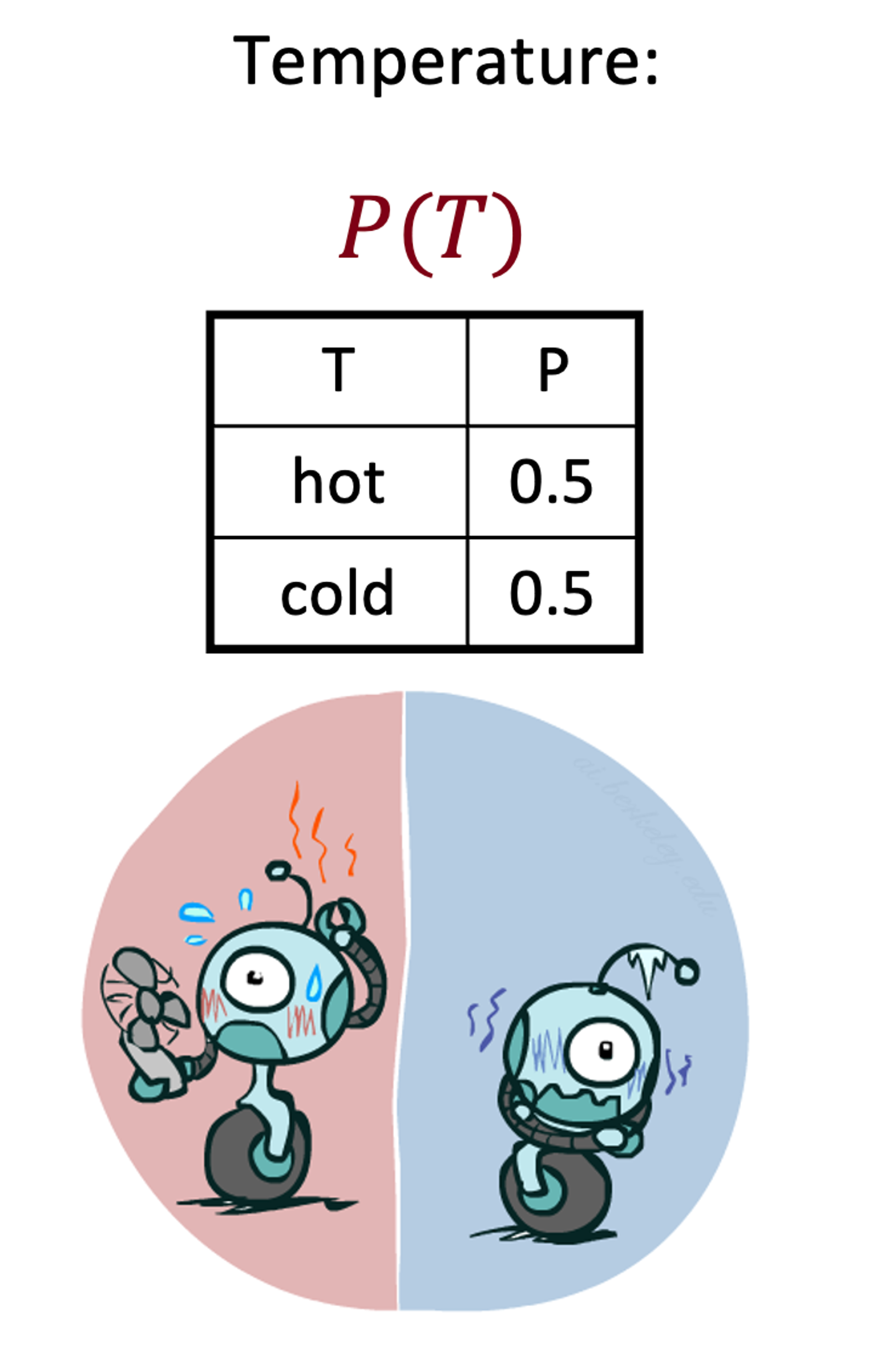


Marginal Distribution
- Marginal Distribution 마진 분포
- 결합 분포에서 관심 없는 변수들을 제거하여 관심있는 변수들만의 분포를 얻는 과정
- 결합 확률 분포에서 특정 변수를 제외시키고 남은 변수들만의 분포
- ex. X, Y에 대판 결합 분포가 있을 때, X의 마진 분포는 Y를 고려하지 않고 X만의 분포를 의미
- Marginalization (summing out)
- 결합 분포에서 한 변수를 ‘합산하여 제거’함으로써 다른 변수의 마진 분포를 얻는 과정
- 결합 분포 테이블에서 차원을 축소하는 것
Conditional distribution
- Conditional probability 조건부 확률
- Conditional Distribution 조건부 분포
- 한 변수 집합에 대한 확률 분포가, 다른 변수 집합의 특정 값에 주어질 때 어떻게 변하는지
- Normalizing a Distribution 정규화
Product and chain rules
- Product Rule
- 두 사건이 독립적일 경우 P(A∩B)=P(A)×P(B)
- 독립적이지 않을 경우 P(A∩B)=P(A)×P(B∣A)
- Chain Rule
- 결합 확률 분포를 조건부 확률 분포의 곱으로 나타내는 방법
Inference
- Probabilistic inference
- 주어진 근거에 기반하여 확률 모델로부터 원하는 확률을 계산하는 과정
- 쿼리 변수에 대한 확률을 계산할 때, 그 변수가 특정 증거가 주어졌을 때의 확률로 정의
- 확률적 모델을 활용하여 불확실성 하에 의사결정을 내리는 많은 응용 분야에서 사용
- Inference by Enumeration
- 증거 변수 Evidence variables
- 이미 알려진 값 또는 관찰된 값
- 추론 과정에서 고정되며, 쿼리 변수의 확률을 계산할 때 기준점으로 사용
- 쿼리 변수 Query variables
- 확률을 알고싶어하는 변수
- 숨겨진 변수 Hidden variables
- 증거나 쿼리 변수로는 나타나지 않지만 시스템의 동작에 영향을 미칠 수 있는 변수
- 증거 변수 Evidence variables
- Bayes’ Rule 베이즈 정리
- 주어진 증거를 바탕으로 가설의 확률을 업데이트하는 방법 제공
- 어떠한 조건부 확률을 직접 계산하기 어려울 때, 더 계산하기 쉬운 반대 조건부 확률과 주변 확률을 사용하여 원하는 조건부 확률을 유도
Independence
- Independence 독립
- 변수들간의 관계를 단순화
- 두 변수가 독립일 때
- ∀x,y, P(x,y)=P(x)P(y)
- P(x∣y)=P(x)orP(y∣x)=P(y)
- 실제 세계에서 변수들 간의 완전한 독립성은 거의 없음
- 조건부 독립성
- 주어진 조건 하에서 두 변수가 독립적
- 흔함
Conditional independence
- Conditional Independence 조건부 독립
- ∀x,y,z, P(x∣y,z)=P(x∣z)
- ∀x,y,z, P(x,y∣z)=P(x∣z)P(y∣z)
'인공지능 > Artificial Intelligence (COSE361)' 카테고리의 다른 글
| [인공지능] Chapter 15. Decision Network (0) | 2023.12.19 |
|---|---|
| [인공지능] Chapter 14. Bayesian Network (0) | 2023.12.19 |
| [인공지능] Chapter 12. Reinforcement Learning (2) (3) | 2023.12.06 |
| [인공지능] Chapter 11. Reinforcement Learning (1) (2) | 2023.12.04 |
| [인공지능] Chapter 10. Markov Decision Process (2) (2) | 2023.11.27 |


