Double Bandits
- Double bandits
- 강화학습의 한 영역
- 두 가지 알고리즘이 결합된 형태
- 1st bandit
- 탐험
- 환경과의 상호작용을 통해 가장 효과적인 행동을 선택하려고 함
- 알려지지 않은 환경에서 가장 좋은 결과를 얻기 위해 다양한 행동을 시도하는 과정
- 2nd bandit
- 활용
- 이러한 탐험을 통해 얻은 데이터를 기반으로 가장 효과적인 데이터를 예측
- 이미 알려진 정보를 활용하여 가장 좋은 결과를 얻는 것을 목표로 함
- 1st bandit
- 위 두 가지 접근 법 사이의 균형을 맞추는 것이 Double bandits의 핵심 문제
Offline Planning
- offline planning
- 환경에 대한 전체 정보를 갖고 있을 때 주로 사용
- 미리 모든 가능한 상태와 행동에 대한 가치를 계산하고, 이를 바탕으로 최선의 정책을 결정
- 시뮬레이션, 게임, 등 잘 알려진 환경에서 사용
- 단: 높은 계산 비용
- 장 실제 환경에서 행동을 시작하기 전에 최적의 행동을 결정할 수 있음
- Solving MDPs is offline planning
- 계산을 통해 모든 quantities 결정
- MDP의 details를 알아야함
- 실제로 play하는 것은 아님
Online Planning
- online planning
- 실시간으로 정보를 받아들이며 행동을 결정하는 경우에 사용
- 현재 상태에서만 최적의 행동을 계산 → 이를 바탕으로 다음 행동 결정
- 실시간 시스템, 로봇 공학, 불확실한 환경에서 활용
- 장: 낮은 계산 비용
- 단: 매 순간마다 최적의 행동을 계산해야 함
Initially unknown MDPs
- unknown MDP(Markov Decision Process)를 다룰 때 강화학습에서 고려해야할 요소
- Exploration (탐험)
- 처음에는 환경에 대한 정보가 없기 때문에 어떤 행동이 최적인지 알기 위해 다양한 시도를 해야함 (1st bandit)
- Exploitation (활용)
- 일정 시간 동안 환경을 탐험하고 데이터를 수집한 후, 그 정보를 기반으로 최적의 행동을 선택 (2nd bandit)
- Regret (후회)
- 초기에 환경에 대한 정보가 부족하여, 잘못된 행동을 선택하여 보상을 잃는 경우가 발생
- Sampling
- 최적의 행동을 결정하기 위해, 동일한 행동을 여러 번 반복하여 그 결과를 관찰
- Generalization (일반화)
- 한 상태에서 배운 것이 다른 상태에도 적용될 수 있음
- Exploration (탐험)
Reinforcement learning
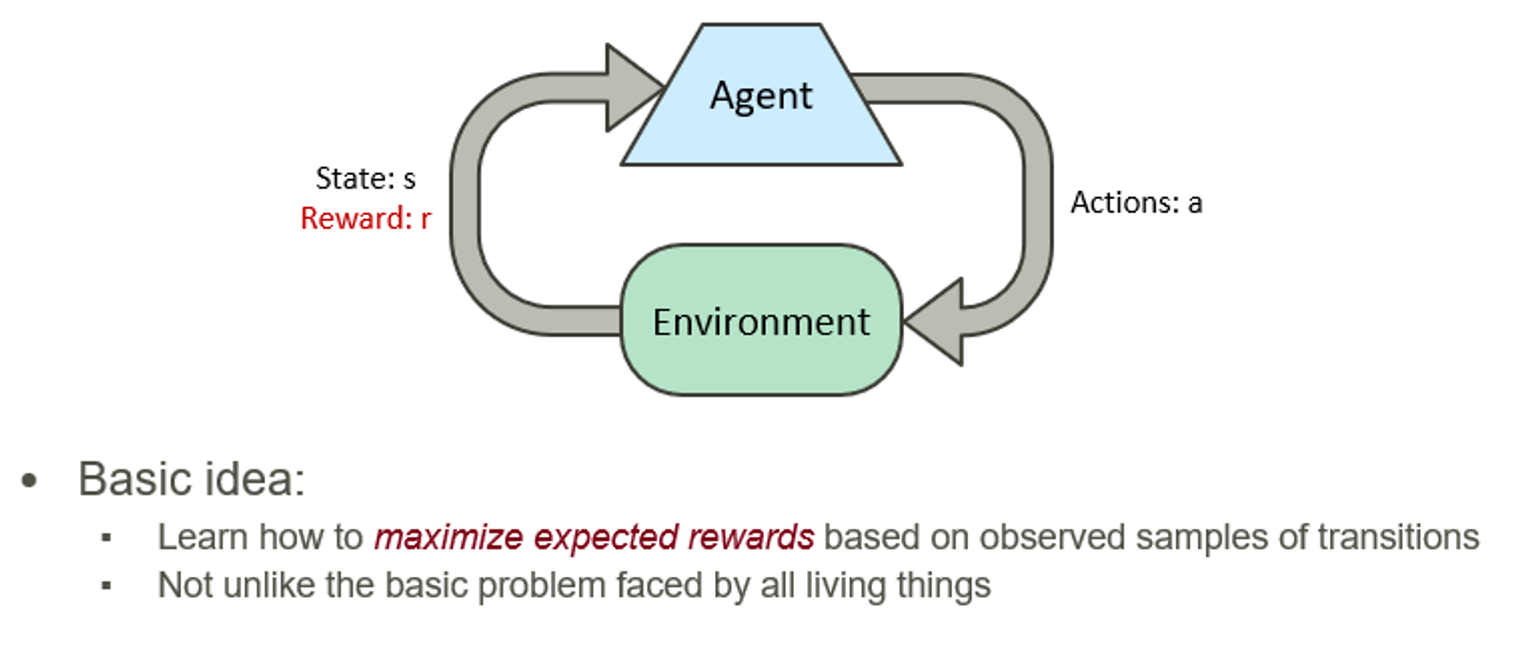
- Basic idea
- 관찰된 transitions의 샘플들을 바탕으로 기대 보상을 최대화 하는 방법 학습
- Not unlike the basic problem faced by all living things
- 에이전트가 환경과 상호작용하면서 최적의 행동을 학습
- 벌과 보상을 통해 학습
- MDP를 기본 가정으로 함
- A set state s
- 에이전트가 있는 환경의 특정 상태
- ex: 체스 게임에서 보드의 현재 위치
- A set of actions A(s)
- 에이전트가 특정 상태에서 취할 수 있는 모든 가능한 행동의 집합
- A transition model T(s, a, s’)
- 전이 모델
- 에이전트가 특정행동 a를 취했을 때, 상태 s에서 상태 s’로 변할 확률
- A reward function R(s, a, s’)
- 보상 함수
- 에이전트가 행동 a를 취해 상태 s에서 상태 s’로 전이했을 때 받는 보상
- A set state s
- 정책 π(s)
- 에이전트가 특정 상태에서 어떤 행동을 취할 것인지를 결정하는 전략
- 최적의 정책은 각 상태에서 가능한 최대의 기대 보상을 주는 행동을 선택
- 강화학습의 어려움
- 전이 모델 T와 보상 함수 R을 알 수 없다
- 에이전트가 어떤 상태에서 높은 보상을 받는지, 특정 행동이 어떤 결과를 초래할 지 미리 알 수 없음 → 따라서 에이전트는 새로운 상태와 행동을 탐색해야함 (이 과정을 ‘탐험’이라고 함)
- 전이 모델 T와 보상 함수 R을 알 수 없다
- Approaches to Reinforcement Learning
- Model-based
- learn the model, solve it, execute the solution
- 에이전트가 환경에 대한 모델을 학습하고, 이를 통해 문제를 해결
- 에이전트는 전이 확률과 보상을 추정하고, 이를 통해 최적의 정책을 탐색
- Learn values from experiences, used to make decisions
- 에이전트가 경험을 통해 상태 또는 행동의 가치를 학습하고, 이를 바탕으로 결정을 내리는 방식
- 각 행동이 미래의 보상에 어떤 영향을 미치는지 알 수 있음
- Direct evaluation
- 에이전트가 여러 번의 시도를 통해 행동의 평균 보상을 계산하고 이를 통해 행동의 가치를 추정하는 방식
- Temporal difference learning
- 에이전트가 현재 상태의 가치 추정치와 다음 상태의 가치 추정치 사이의 차이, 즉 ‘히간적 차이’를 이용해 가치를 업데이트
- 보상과 다음 상태의 가치 추정치를 즉시 반영하기 때문에 실시간 학습이 가능
- Q-learning
- 에이전트가 특정 상태에서 특정 행동을 취했을 때의 기대보상, 즉 Q-value를 학습하는 방법
- Q-value를 통해 행동을 결정하며, 전이 모델이나 보상 함수를 알지 못해도 학습이 가능
- Direct evaluation
- Learn policies directly
- 에이전트가 가치 추정 없이 직접적으로 정책을 학습하는 방법
- Model-based
Model-based learning
- Model-based learning
- Idea
- 에이전트가 경험을 통해 환경에 대한 근사 모델을 학습
- 이 모델을 정확하다고 가정하고 가치를 계산
- 에이전트가 환경에 대한 모델을 학습하고 이를 통해 최적의 행동을 결정하는 방법
- 환경에 대한 사전지식이 없는 상황에서 유용
- 실제 환경과 모델 사이의 차이를 최소화하는 방향으로 학습이 진행됨
- Step 1: Learn empirical MDP model
- 에이전트가 경험을 통해 MDP 모델을 학습
- 각 상태 s와 행동 a에 대한 결과 s’를 카운트하고, 이를 통해 전이 확률 T(s, a, s’)를 추정
- 에이전트는 전이가 발생했을 때 보상 R(s, a, s’)을 발견
- Step 2: Solve the learned MDP
- 학습된 MDP를 해결
- 가치 반복이나 정책 반복 같은 기존의 방법 사용
- Idea
- 장점
- 효율적인 경험 활용
- 에이전트가 환경과 상호작용한 경험을 효율적으로 활용
- 샘플 복잡성이 낮음
- 적은 수의 경험을 통해 모델을 학습하고, 이를 통해 환경에 대한 이해를 높임
- 효율적인 경험 활용
- 단점
- 큰 상태 공간에 대한 확장성 부족
- 상태 공간이 매우 큰 경우, 모든 상태를 학습하는 데 어려움을 겪을 수 있음
- 모델 학습에 필요한 계산 및 저장 공간이 증가하기 때문
- 한 번에 하나의 상태-행동 쌍만 학습
- 기본적으로 model-based 학습은 한 번에 하나의 상태-행동 쌍을 학습
- 큰 상태 공간에 대한 MDP 해결 불가
- 상태 공간이 매우 큰 경우, Model-based 학습은 MDP를 해결하는데 어려움을 겪을 수 있음
- 부분적으로 관찰 가능한 환경에서의 어려움
- 환경이 부분적으로만 관찰 가능한 경우, model-based 학습은 모델을 정확하게 학습하는 데 어려움을 겪을 수 있음
- 에이전트는 전체 환경에 대한 정보가 없기 때문에, 모델의 정확도가 떨어질 수 있음
- 큰 상태 공간에 대한 확장성 부족
Model-free learning
- 기대값을 추정하는 방법
- 분포를 추정하고 기대값을 계산
- 먼저 샘플 데이터를 사용해 확률 분포를 추정하고, 이 추정된 분포를 바탕으로 기대값을 계산
- Model-based
- 분포를 건너뛰고 샘플로부터 기대값을 직접 추정
- 확률 분포의 추정 없이 샘플을 사용해 기대값을 바로 추정
- Model-Free
- 분포를 추정하고 기대값을 계산
- Model-free Methods
- 환경에 대한 모델을 학습하는 대신, 에이전트는 경험을 통해 직접 최적의 행동을 학습
- 각 상태와 행동에 대한 보상을 학습하고 이를 바탕으로 정책을 개선
- Q-learning, Monte Carlo 방법 등이 있음
- Passive reinforcement learning
- 주요 목표: 주어진 정책의 효과를 평가
- 에이전트는 주어진 정책에 따라 행동하고, 그 결과로 얻는 보상을 학습하여 이 정책이 얼마나 좋은지 평가
- 에이전트가 환경과 상호작용하면서 학습하지만, 어떤 행동을 취할지 선택하는 능력이 없는 상황
- 에이전트는 주어진 정책을 따르며, 환경에서 주어진 보상을 통해 이 정책의 좋음과 나쁨을 학습
- 에이전트는 정책을 따라 행동하고, 그 결과로 얻는 보상을 통해 환경에 대한 이해를 높임
- ex: 체스 게임에서 에이전트가 특정 전략을 따라 게임을 진행하고, 게임의 결과를 통해 이 전략의 효과를 평가
- Direct Evaluation
- 강화학습에서 사용하는 방법론중 하나
- 특정 상태에서의 예상 총 할인 보상을 추정하는 데 사용됨
- 𝜋는 정책(policy)을, s는 상태(state)
- idea
- return 사용
- ‘return’은 특정 상태 s에서의 실제 할인된 보상의 합
- ‘return’ = 에이전트가 상태 s에서 행동을 취하고, 그 결과로 얻는 보상을 할인 계수를 적용해 합한 값
- 여러 시행과 상태 방문에 대한 평균
- 에이전트는 여러 번의 시행(trial)과 상태 s를 여러 번 방문하면서 얻은 return의 평균을 계산
- 이 평균값이 상태 s에서의 예상 총 할인 보상의 추정치가 됨
- return 사용
- 장점
- 이해하기 쉽다
- 상태를 방문할 때마다 보상을 측정하고, 이를 바탕으로 해당 상태의 가치를 추정
- 전이 함수 T나 보상 함수 R에 대한 지식이 필요하지 않다
- 한계에서 올바른 답으로 수렴한다
- 이해하기 쉽다
- 단점
- 각 상태를 별도로 학습해야함
- 상태 연결에 대한 정보를 무시한다
- 학습에 오랜 시간이 소요된다
- Temporal difference learning (TD)
- 시간차 학습 (model-free mothod)
- 에이전트가 현재 상태의 가치 추정치와 다음 상태에서의 실제 보상을 비교함으로써 현재 상태의 가치 추정치를 업데이트 하는 방법
- 각 에피소드가 끝나기를 기다리지 않고 각 단계에서 바로 가치를 업데이트
- 부분적으로 완료된 에피소드로부터 학습이 가능 → 더 빠른 학습
- 현재 상태 가치 V(s)와 실제로 얻은 보상과 다음 상태의 가치의 합인 R(s, a, s') + γV(s') 간의 차이, 즉 "시간차 오류"를 사용하여 가치를 업데이트
- α는 학습률(learning rate)이며, γ는 할인계수(discount factor)
- idea
- 실제 샘플을 사용하여 기대값을 추정
- 각 전이 s, a, s’, r 이후에 s의 값을 업데이트
- 실행 평균(runing average)을 유지하며 값을 업데이트
- Running Average
- 데이터 스트림의 평균을 계산하는 방법
- 새로운 데이터가 들어올 때마다 이전의 평균에 새로운 데이터를 반영하여 평균을 계산
- 데이터가 시간에 따라 변화하는 경우나 전체 데이터를 한 번에 처리할 수 없는 상황에서 유용하게 사용
- 방법
- 초기 평균은 첫 번째 데이터 값으로 설정
- 새로운 데이터가 들어올 때마다, 이전 평균과 새로운 데이터 값을 이용하여 새로운 평균을 계산. 이 때, 이전 평균은 이전 데이터 값들의 수를 고려하여 가중치를 부여받고, 새로운 데이터는 1의 가중치를 가짐
- 이 방법은 exponential forgetting이라고도 부름
- 오래된 데이터일수록 그 가중치가 지수적으로 감소하기 때문
- TD value learning의 문제
- TD value learning은 정책 평가를 행하기 위한 model-free 방식.
- Running sample averages의 Bellman update를 모방
- 그러나 상태 전이 모델 없이는 가치 함수를 사용하거나 정책을 개선하는 것이 불가
- 한 단계 탐욕스러운 expectimax를 수행하기 위해서는 상태 전이 모델이 필요하기 때문
- Q-Learning as Approximate Q-iteration
- 강화 학습의 한 방법
- 최적이 아닌 정책에서 샘플을 생성하더라도 최적의 정책으로 수렴
- 주의할 점
- 충분한 탐색 필요
- 모든 상태-행동 쌍을 무한히 시도해야 함
- 모든 가능한 상태-행동을 학습하고 그 결과를 반영하여 최적의 정책을 찾아가기 위함
- 학습률을 너무 빨리 줄이지 않아야 함
- 학습률이 너무 빨리 줄어들면, 에이전트가 학습을 충분히 하지 못하고 최적의 정책을 찾지 못할 수도 있음
- 충분한 탐색 필요
Summary
- RL은 trainsitions(전이)와 rewards(보상)에 대한 직접적인 경험을 통해 MDP를 해결
- MDP 모델을 학습하고 이를 해결
- 보상의 합계로부터 직접 V를 학습하거나, TD 로컬 조정을 통해 학습 (하지만 미래를 내다보며 결정을 내리기 위해서는 여전히 모델이 필요)
- 로컬 Q-Learning 조정을 통해 Q를 학습하고, 이를 직접 사용하여 행동을 선택
- 해결해야할 큰 문제
- 어떻게 하면 regret 없이 탐색을 할 수 있을까?
- 이는 탐색과 활용의 균형 문제로, 에이전트가 새로운 정보를 얻기 위해 탐색을 수행하면서도 최적의 행동을 활용해야 하는 문제를 의미
- 어떻게 하면 테트리스나 스타크래프트처럼 큰 규모로 확장할 수 있을까?
- 이는 상태 공간이나 행동 공간이 매우 큰 문제에서 강화학습을 어떻게 효과적으로 적용할 수 있을지에 대한 문제
- 어떻게 하면 regret 없이 탐색을 할 수 있을까?
'인공지능 > Artificial Intelligence (COSE361)' 카테고리의 다른 글
| [인공지능] Chapter 13. Probability (1) | 2023.12.18 |
|---|---|
| [인공지능] Chapter 12. Reinforcement Learning (2) (3) | 2023.12.06 |
| [인공지능] Chapter 10. Markov Decision Process (2) (2) | 2023.11.27 |
| [인공지능] Chapter 9. Markov Decision Process (1) (1) | 2023.10.25 |
| [인공지능] Chapter 8. Adversarial Search (2) (0) | 2023.10.25 |



